Таблица части, Расширяющиеся деревья и «Трейлы» (боже мой!)
Перевод статьи - Piece Tables, Splay Trees, and
Автор - Эйвери Лэрд (Avery Laird)
Источник оригинальной статьи:
http://www.averylaird.com/programming/piece-table/2018/05/10/insertions-piece-table/#code
Это было намного сложнее, чем я думал (и если Вы не уверены, что “это", проверьте мой последний пост). Во-первых, я попытался использовать красно-черное дерево для хранения кусков, аналогично методу, предложенному Хоакином Куэнкой Абелой. Он уже написал очень впечатляющую реализацию на C++. Предостережение с красно-черными деревьями заключается в том, что у них много случаев, и (в большинстве ситуаций) они работают только немного лучше, чем некоторые альтернативы. И, как когда-то мудро было сказано:
“... преждевременная оптимизация - корень всего зла”.
Дональд Нут
Когда вы думаете о сбалансированных бинарных деревьях, всегда есть три основные структуры для рассмотрения: деревья AVL, деревья splay и нормальные (несбалансированные) деревья BST. Может показаться противоречием включение несбалансированных BST в список сбалансированных деревьев; однако веб-сайты могут оставаться сбалансированными до тех пор, пока вставляемые ключи достаточно несортированы. Текстовый редактор обычно не соответствует этому требованию.
Деревья AVL обычно работают очень хорошо, почти так же, как и красно-черные деревья. Если вы не уверены в характере данных, хранящихся в дереве, дерево AVL прекрасно работает. Мы можем работать немного умнее, хотя есть более простое и быстрое решение: Splay trees. Эта структура перераспределяет узлы дерева, похожие на деревья AVL. Главное отличие состоит в том, что мы не стремимся балансировать дерево вообще - мы продолжаем перемещаться вокруг («разглаживая») узлы, пока последний вставленный узел не станет корнем дерева. И как я объясню ниже, мы можем «кодировать» позиции фигур в структуре дерева, устраняя необходимость отслеживать индексы.
На первый взгляд может показаться, что деревья с пауками не должны работать хорошо, возможно, даже хуже, чем UBST, потому что они не особенно сбалансированы. Удивительно, что амортизированная временная сложность операций в дереве splay - O(logN). Это объясняется тем, что деревья Splay полагаются на предположение о том, что в последнее время данные о наиболее часто запрашиваемых данных, скорее всего, потребуются в будущем. Это, как правило, верно, но особенно актуально в случае текстовых редакторов. В большинстве случаев мы работаем только с небольшим разделом документа.
Части Atom были недавно переписаны, чтобы использовать дерево splay, с явно хорошими результатами. Я знаю, что деревья Splay будут очень хорошо работать с общим вариантом использования - я не уверен, как они будут работать с большими буферами и несколькими курсорами / параллельными редакторами. Есть только один способ узнать.
“Один хороший тест стоит тысячу мнений эксперта”.
Вернхер Фон Браун
Операции
При проектировании буферного интерфейса необходимо учитывать две основные функции:
insert(index,string) (1)
elete(span) (2)
A span заказанный набор двух индексов, (is,ie) который представляет все знаки в пределах того ряда индексов (включительно). На этой почте я буду обращаться только с операцией по вставке и обращаться к удалению на более поздней почте.
index известен нам через позицию курсора, и string дан вводом данных пользователем наряду с span. Все другие ценности должны быть обработаны внутренне. Мы храним информацию о, редактирует в столе части, абстрактно; но фактически, так как мы держим каждую часть в дереве, это - больше “дерева части” (или “трейл?”). Есть некоторые условия, которые мы должны поместить на это дерево, главным образом, что обход по порядку, начиная с корня дерева, приводит к правильной оценке буфера. Поскольку узел эквивалентен куску, а дерево эквивалентно таблице, я буду использовать эти термины взаимозаменяемо (в зависимости от того, что наиболее подходит в контексте).
Хотя мы можем правильно оценить всю таблицу, начиная с корня и любого раздела буфера, пройдя дочерний узел и его поддеревья, мы не знаем, где раздел принадлежит буферу. Как я объясню, нет способа узнать положение узла в буфере без какой-либо информации о остальной части дерева. Это связано с тем, что мы будем использовать очень умное предложение от Хоакина Абелы, которое позволяет нам хранить узлы на основе их относительного индекса - их индекса по отношению к другим частям в таблице.
Чтобы реализовать этот метод, необходимо внести два изменения в типичное дерево splay: как мы вставляем узлы и как мы храним данные. На процедуру вставки узлов влияет ключ, который мы выбираем для сортировки данных. Интуитивно это должно быть связано с положением части документа. Сначала мы могли бы рассмотреть использование желаемого индекса вставки, id.
Проблема с использованием id заключается в том, что он должен измениться для любой вставки в индексе i ≤ id. После такой вставки нам нужно обновить каждый узел после i. В случае нескольких вставок в начале существующего буфера это означает сложность времени O(n) для каждой вставки - не лучше, чем массив.
Хоакин Абела предлагает решение этой проблемы: хранить информацию о смещении в самих узлах. Он делает это, сохраняя размеры поддеревьев, а не индексы:
Explicit Indexing Relative Indexing
n1 n1
index: 14 size_right: 1
length: 10 size_left: 14
/ \ => length: 10
n2 n3 / \
index: 0 index: 23 n2 n3
length: 14 length: 1 size_right: 0 size_right: 0
/ \ / \ size_left: 0 size_left: 0
A B C D length: 14 length: 1
/ \ / \
A B C DСтоит провести немного времени, говоря о примере выше, потому что есть два очень важных различия, чтобы рассмотреть. Во-первых, отметьте это n2 имеет индекс 0 и длина 14, в то время как n1 берет в индексе 14. Это вызвано тем, что размер 1-индексируем (я не рассматриваю последовательности длины 0 иметь значение), тогда как индекс 0-индексируем. Так, n2 фактически индексы промежутков 0 -> 13. Я также определю вставку в индексе ii иметь следующее поведение:
0123456789ABCDEFGH
This is a sentence
^ insert 'i' @ index D
This is a senitenceТаким образом, индекс i относится к желаемой конечной позиции.
Во-вторых, и самое главное, обратите внимание на то, как структура дерева не меняется в любом случае. Это иллюстрирует, как сама структура дерева хранит правильный порядок частей относительно друг друга и подразумевает, что любые ресурсы, потраченные на хранение и обновление индекса, являются отходами. В отличие от индексов, этот порядок также является постоянным даже после разыгрывания - как только узел вставлен правильно, все работает нормально.
Наконец, нам нужно рассмотреть вопрос о том, как вставленная деталь может потребовать «расщепления» существующей части. Это включает в себя разработку теста, чтобы определить, когда должен произойти раскол, и выполнить разделение таким образом, чтобы сохранялись все свойства таблицы кусков и дерева разделов (я не буду давать особенно подробного объяснения деревьев пауз здесь, но Wikipedia страница - хорошее место для начала).
Вставки
Чтобы сделать вставку, нам все равно нужно будет рассмотреть желаемый индекс, но мы можем его забыть потом. Я рассмотрю пример ниже. Мы будем использовать тот же пример, что и выше, если предположить, что существующий буфер был вставлен как одна часть.
(1) Original Tree (2) Insert 'i' @ index 13
size_right: 0 size_right: 0 Because:
size_left: 0 size_left: 0 offset length: 18 we must split!
text: 0x0 text: 0x0
(2.1) View of subtree during split
/
size_right: 0
size_left: 13
length: 1
text: 0x1
/
size_right: 0
size_left: 0
length: 13
text: 0x2
(2.2) Join split subtree with parent node
size_right: 0
size_left: 0 <-- must update size_left
length: 18 <-- must update length
text: 0x0 <-- must update text pointer
/
size_right: 0
size_left: 13
length: 1
text: 0x1
/
size_right: 0
size_left: 0
length: 13
text: 0x2
(2.3) Update parent node
size_right: 0
size_left: 19 <-- 13+1+5
length: 5 <-- 18-13
text: 0x3 <-- explained below
/
size_right: 0
size_left: 13
length: 1
text: 0x1
/
size_right: 0
size_left: 0
length: 13
text: 0x2 Конечно, есть фактически (до) 3 разных способа выполнить такой раскол. Я выбираю создать связанный список на той стороне, которую должен быть вставлен узел, потому что мы знаем, что там нет никаких детей. Другая вещь, которую следует учитывать, - это то, как память управляется повсюду. Если мы рассмотрим только упомянутые выше адреса памяти, мы увидим что-то вроде этого:
(1) 0x0: This is a sentence
(2.1) 0x0: This is a sentence
0x1: i
(2.2) 0x0: This is a sentence
0x1: i
0x2: This is a sen
(2.3) 0x0: This is a sentence <-- here we can free(0x0)
0x1: i
0x2: This is a sen
0x3: tenceЭтот метод может быть сделан, не копируя, если мы также храним a start стоимость в узле. Мы все еще должны ассигновать память для недавно вставленного характера, но мы никогда не должны были бы изменять указатель на память, как только это ассигновано. Мы можем просто увеличить start стоимость, чтобы быть безотносительно длины первого узла в разделении. Например, следующее содержание памяти и указатель /start пары:
0x0 This is a sentence
0x1 i
0x0, start = 0 , length = 13
0x1, start = 1 , length = 1
0x0, start = 13, length = 5start стоимость была бы относительно текстового указателя. Мы можем получить часть текста, который мы хотим, читая text+start от sizeof(text_type)*length байты (данные, которые мы храним, могут или могут не быть a char).
Наконец, если мы делаем inorder пересечение дерева в качестве примера, мы добираемся:
This is a senitence
|-----------|||---|
piece1 | |
piece2----| |
piece3-------|Вставка без разделения сформировала бы поддерево единственного узла и выполнила бы ту же самую операцию по соединению. Однако только size_left из родительского узла (в этом случае) был бы изменен — length и start ценности не изменились бы. Фактически, если мы будем следовать за процессом, описанным выше, то разделение будет всегда присоединяться левой стороны родителя, потому что желаемый индекс вставки - меньше, чем промежуток той части.
Код
Сначала нам понадобится кусок, который представляет собой лишь совокупность трех значений:
typedef struct Piece {
unsigned long start, length;
char *text;
};Я предполагаю, что мы будем хранить char здесь, но мы можем заменить ее другой тип позже, если надо. Мы будем хранить эти части в древовидной структуре
struct Tree {
struct Piece *piece;
struct Tree *left, *right, *parent;
unsigned long size_left, size_right;
};С точки зрения типов, это все. Я не буду постить кучу кода, все это доступно на github. Однако я расскажу о функциях, связанных с вставками, и о том, как я справляюсь с этим процессом.
Во-первых, мы следуем типичному алгоритму вставки BST. Тем не менее, перед выполнением вставки, мы выполняем разделенный тест. Если необходимо выполнить разбиение, мы делаем это, в противном случае просто вставляем узел нормально. Мы записываем адрес только что вставленного узла и передаем его в функцию splay.
Функция splay принимает адрес нового узла и расклеивает его вверх по дереву до тех пор, пока он не станет корнем дерева. Вот и все! Звучало довольно легко для меня в первый раз, когда я пытался написать его. И, может быть, если бы у меня были лучшие кодирующие отбивные, это было бы. Однако через некоторое время мне удалось получить тестируемую базовую реализацию.
Тестирование
Это трудно сделать полезные, комплексные тесты в этом случае, так как есть так много ситуаций, которые могут возникнуть. Однако, я сделал некоторые очень простые тесты и бенчмаркинг insert операции, получая интересные результаты.
Во-первых, я вставил 1 000 000 символов в таблице, что эквивалентно плотной документа с 30 000 страниц, дает следующий график:

Это, конечно, странный вид графа действительно, и это в основном связано с природой дерева splay. Я предполагаю, что прямые линии представляют собой операции, близкие друг к другу, и поэтому очень быстрые. Гораздо медленнее время вставки представляют операции очень далеко от предыдущих, которые затем становятся быстро из-за операции splay. Это не плохо для худшего случая,но не особенно впечатляет. Все становится интересным, если мы посмотрим на другое количество.
Вставка символов случайным образом не дает справедливого представления общего варианта использования для большинства редакторов. Чтобы получить более сбалансированную перспективу, я также записал среднее время для каждой вставки в таблицу определенного размера. Я сохранил Общее время вставки, и после каждой вставки я разделился на текущий Размер таблицы. Это отражает среднее время для каждой вставки до этой точки. Я получил следующий результат:
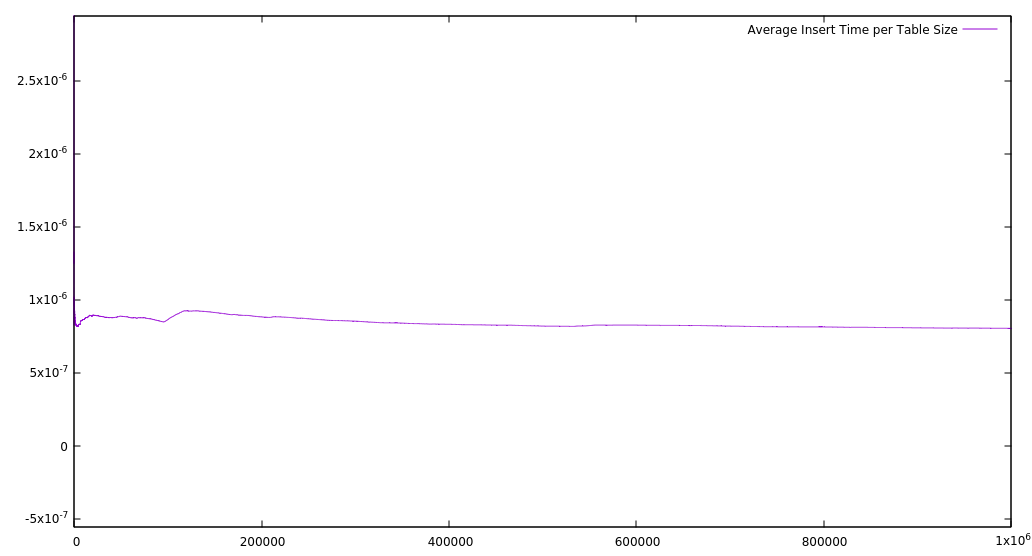
Это говорит о том, что, независимо от размера таблицы, всегда требуется примерно одно и то же время для выполнения вставки, и это результат, который я доволен. Как некоторые простые, предварительные тесты, есть не так много, что можно сделать вывод — возможно, сравнение между другими реализациями (массив, связанный список и т.д.) было бы интересно. Мой внутренний скептик и считает, что время это быстрая, кажется, немного слишком хорошо, чтобы быть правдой, и всегда есть вероятность ошибки, что я не заметил. Я планирую разработать некоторые лучшие тесты, чтобы исключить эту возможность.
Вы можете проверить весь код на github. Следующие грубые шаги-поддержка удаления, отмены, а затем работа над API. После этого несколько курсоров, пользователи-и не только!